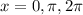Question

Find all solutions of each equation on the interval 0 ≤ x < 2 pi.

tan^2 x sec^2 x +2 sec^2 x -tan^2 x =2

Answer 1

`x=0,\pi,2\pi`

Explanation:

The given equation is:
`\tan^2x\sec^2x+2\sec^2x-\tan^2x=2`.

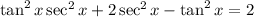Subtract 2 from both sides

`\tan^2x\sec^x+2\sec^2x-\tan^2x-2=0`.

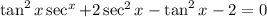Factor by grouping:

`\sec^2x(\tan^2x+2)-1(\tan^2x+2)=0`.

`(\sec^2x-1)(\tan^2x+2)=0`.

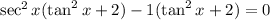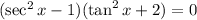Apply the zero product principle:

`(\sec^2x-1)=0\:\:or\:\:(\tan^2x+2)=0`.

`\sec^2x=1\:\:or\:\:\tan^2x=-2`.

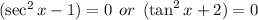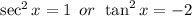If
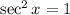`\sec^2x=1`, then
`\sec x=\pm 1`,

`\implies \cos x=\pm1`

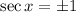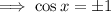
This implies that:
`x=0,\pi,2\pi`

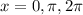
If
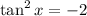`\tan^2x=-2`, x is not defined for all real values.

Therefore the required solution on the given interval
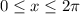`0\le x\le2\pi` is
`x=0,\pi,2\pi`