Question

A polynomial function has a root of -6 with multiplicity 3 and a root of 2 with multiplicity 4 if the function has a negative leading coefficient and is of odd degree which could be the graph of the function

Answer 1

A. -(x + 6)^3 (x - 2)^4

Explanation:

Answer 2

See graph

Explanation:

Let p(x) be the polynomial.

Since -6 is a root with multiplicity 3,
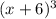`(x+6)^3` is a factor of p(x).

Since 2 is a root with multiplicity 4,
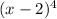`(x-2)^4` is a factor of p(x).

This implies that:

`p(x)=a(x+6)^3(x-2)^4`

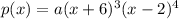
Since a<0, and the degree of the polynomial is odd(4+3=7), the graph falls on the left and also falls to the right.

In other words, the graph approaches positive infinity on the left an negative infinity on the right.

See attachment.