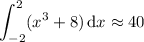Question

Calculus question. Please complete and explain the following.

Answer 1

We're approximating the area under the graph of the function
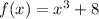`f(x)=x^3+8` over the interval [-2, 2] by

1. partitioning the integration interval into
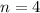   `n=4` subintervals,
2. building rectangles whose lengths are equal to the length of the corresponding subinterval and whose heights are equal to the value of
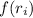   `f(r_i)`, where
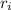   `r_i` denotes the right endpoint of the
   `i`-th subinterval, and
3. computing the areas of each rectangle and adding these areas together.

Splitting [-2, 2] into 4 intervals gives

[-2, -1], [-1, 0], [0, 1], [1, 2]

Each subinterval has length 1. The right endpoints of the
`i`-th subinterval, where
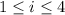`1\le i\le4`, are given by the (arithmetic) sequence

`r_i=-1+1(i-1)=i-2`

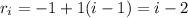
The area of the rectangle over the
`i`-th subinterval is

`A_i=f(i-2)=(i-2)^3+8=i^3-6i^2+6i`

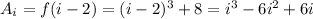
and so the definite integral is approximately

`\displaystyle\int_(-2)^2(x^3+8)\,\mathrm dx\approx\sum_(i=1)^4(i^3-6i^2+6i)`

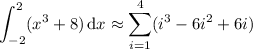
There are well-known formulas for computing the sums of powers of consecutive (positive) integers. The ones we care about are

`\displaystyle\sum_(i=1)^ni=\frac{n(n+1)}2`

`\displaystyle\sum_(i=1)^ni^2=\frac{n(n+1)(2n+1)}6`

`\displaystyle\sum_(i=1)^ni^3=\frac{n^2(n+1)^2}4`

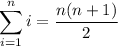
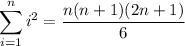
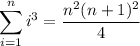
So we get

`\displaystyle\int_(-2)^2(x^3+8)\,\mathrm dx\approx40`