Question

A student scores 74 on a geography test and 249 on a mathematics test. The geography test has a mean of 80 and a standard deviation of 5. The mathematics test has a mean of 300 and a standard deviation of 34. If the data for both tests are normally​ distributed, on which test did the student score better relative to the other students in each​ class?

Answer 1

In geography test.

Explanation:

We have been given that a student scores 74 on a geography test. The geography test has a mean of 80 and a standard deviation of 5. The student scores 249 on a mathematics test. The mathematics test has a mean of 300 and a standard deviation of 34.

Let us find z-scores for both data points. The z-score tells that a data point is how many standard deviation above or below mean.

`z=(x-\mu)/(\sigma)`, where,

z = z-score,

x = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

`z=(74-80)/(5)`

`z=(-6)/(5)`

`z=-1.2`

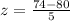
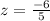
Let us find z-score for mathematics test score.

`z=(249-300)/(34)`

`z=(-51)/(34)`

`z=-1.5`

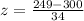
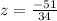
Since z-score for geography test is
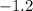`-1.2`, so student was 1.2 standard deviation below mean.

Since z-score for mathematics test is
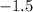`-1.5`, so student's score was 1.5 standard deviation below mean.

Therefore, the student did better on geography test relative to the other students in each​ class.