Question

Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 meters ×80 meters. How much shorter is the root across the park than the route around its edges?

Pls help!!! It's due today in about 6 hours!!!!! I would also like a proper explanation instead of the answer itself!!!!

Answer 1

The route across the park is 40 meter shorter than the route around its edges.

Explanation:

We have to calculate the distance for both routes

As the route around the edges is straight, we have to find the sum of length of both edges

Let
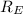`R_E` be the distance of route around edges

`R_E = 80+60 = 140\ meters`

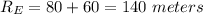
Now we know that a diagonal divides a rectangle in two right angled triangles in which the diagonal is the hypotenuse.

We can use Pythagoras theorem to find the length of the diagonal

So,

`H^2 = P^2 + B^2`

In the given scenario

P = 60

B = 80

Now

`H^2 = (60)^2 + (80)^2\\H^2 = 3600+6400\\H^2 = 10000\\√(H^2) = √(10000)\\H = 100\ meters`

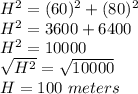
In order to calculate that how much shorter is the path across the park, we have to subtract the distance across park from the distance across edges.

`= 140-100 = 40\ meters`

Hence,

The route across the park is 40 meter shorter than the route around its edges.