Question

A line passes through (9, –9) and (10, –5).Write an equation for the line in point-slope form.

Rewrite the equation in standard form using integers.

A) y + 9 = 4(x + 9) ; -4x + y = -45
B) y - 9 = 4(x + 9) ; -4x + y = 45
C) y - 9 = 4(x + 9) ; -4x + y = -45
D) y + 9 = 4(x + 9) ; -4x + y = 45

^^ The options look pretty similar, so please make sure you're answering correctly! Thank you :)

Answer 1

bearing in mind that standard form for a linear equation means

• all coefficients must be integers, no fractions

• only the constant on the right-hand-side

• all variables on the left-hand-side, sorted

• "x" must not have a negative coefficient

`\bf (\stackrel{x_1}{9}~,~\stackrel{y_1}{-9})\qquad (\stackrel{x_2}{10}~,~\stackrel{y_2}{-5}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{-5-(-9)}{10-9}\implies \cfrac{-5+9}{1}\implies \cfrac{4}{1}\implies 4`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-(-9)=4(x-9)\implies\underline{y+9=4(x-9)} \\\\\\ y+9=4x-36\implies y=4x-45\implies \stackrel{standard~form}{\underline{-4x+y=-45}}`

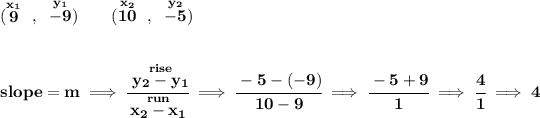
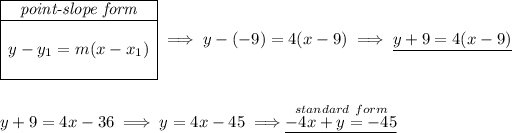
quick note:

the "x" must not have a negative coefficient for the standard form, though in this case it shows like so in the inappropriate choices above.