Question

The weights of pink salmon in a fishery are normally distributed, with a mean of 3.25 pounds and a standard deviation of 0.25 pounds.

What is the probability that a salmon weighs between 2.95 pounds and 3.95 pounds?
A) 0.12
B) 0.38
C) 0.62
D) 0.88

Answer 1

0.88

Explanation:

Given : The weights of pink salmon in a fishery are normally distributed, with a mean of 3.25 pounds and a standard deviation of 0.25 pounds.

To Find : What is the probability that a salmon weighs between 2.95 pounds and 3.95 pounds?

Solution:

We will use z score to find the probability that a salmon weighs between 2.95 pounds and 3.95 pounds

Formula :
`z=(x-\mu)/(\sigma)`

`\mu = 3.25\\\sigma = 0.25`

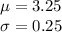
At x = 2.95

`z=(2.95-3.25)/(0.25)`

`z=-1.2`

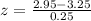
Refer the z table for p value

P(Z<-1.2) =0.1151

At x = 3.95

`z=(3.95-3.25)/(0.25)`

`z=2.8`

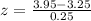
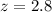
Refer the z table for p value

P(Z<2.8) =0.9974

P(2.95<x<3.95)=P(-1.2<z<2.8)=P(z<2.8)-P(z<-1.2) = 0.9974-0.1151 = 0.88

Hence the probability that a salmon weighs between 2.95 pounds and 3.95 pounds is 0.88