A uniform circular ring has charge Q= 7.36 μC, and radius r = 3.33 cm. Calculate the magnitude of the electric field at a distance of 4.20 cm along the axis of the ring.

Question

asked Aug 14, 2020 78.8k views

2 Answers

Graup · Answer 1 · 2020-08-16T08:25:42+0000

Answer:

The magnitude of the electric field is
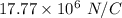
$17.77*10^(6)\ N/C$

Step-by-step explanation:

Given that,

Charge
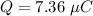
$Q = 7.36\ \mu C$

radius r = 3.33 cm

Distance a = 4.20 cm

We need to calculate the distance d

According to figure

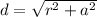
d=√(r^2+a^2)

We need to calculate the electric field

Using formula of electric field

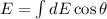
$E=\int{dE\cos\theta}$

$E=\int{(k dq)/(d^2)\cos\theta}$

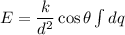
$E=(k)/(d^2)\cos\theta\int{dq}$

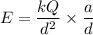
E=(kQ)/(d^2)*(a)/(d)

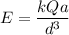
E=(kQa)/(d^3)

Put the value into the formula

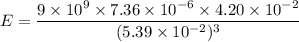
E=(9*10^(9)*7.36*10^(-6)*4.20*10^(-2))/((5.39*10^(-2))^3)

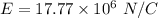
$E=17.77*10^(6)\ N/C$

Hence, The magnitude of the electric field is [tex]17.77\times10^{6}\ N/C[/tex]

Briggs · Answer 2 · 2020-08-20T02:07:01+0000

Answer:

Electric field,
$E=1.80* 10^7\ N/C$

Step-by-step explanation:

It is given that,

Charge on the ring,
$Q=7.36\mu C=7.36* 10^(-6)\ C$

Radius of ring, r = 3.33 cm = 0.0333 m

Distance from axis of ring, x = 4.2 cm = 0.042 m

The electric field at the axis of ring is given by :

E=(kxQ)/((x^2+r^2)^(3/2))

E=(9* 10^9* 0.042* 7.36* 10^(-6))/((0.042 ^2+0.0333 ^2)^(3/2))

$E=1.80* 10^7\ N/C$

So, the magnitude of electric field is
$1.80* 10^7\ N/C$ . Hence, this is the required solution.