Answer:
The ratio of its corresponding sides is
![\sqrt[3]{21}](https://img.qammunity.org/2020/formulas/mathematics/high-school/iu4myireq0izna2vb1mwoswytuisgm3ps8.png)
Explanation:
we know that
If two solids are similar, then the ratio of its corresponding sides is proportional and this ratio is called the scale factor. And the ratio of its volumes is equal to the scale factor elevated to the cube
Let
z ----> the scale factor
x ----> the volume of the larger solid
y ----> the volume of the smaller solid
so
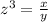
we have


substitute
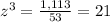
![z=\sqrt[3]{21}](https://img.qammunity.org/2020/formulas/mathematics/high-school/7lobuk8idr1vzwv9qqdmoq1y6xm1jp9gec.png)
therefore
The ratio of its corresponding sides is
![\sqrt[3]{21}](https://img.qammunity.org/2020/formulas/mathematics/high-school/iu4myireq0izna2vb1mwoswytuisgm3ps8.png)