Question

Suppose that a poll of 18 voters is taken in a large city. The random variable x denotes the number of votes who favor a certain candidate for mayor. Suppose that 43% of all the city's voters favor the candidate. Find the probability that exactly 10 of the sampled voters favor the candidate. (round to three decimal places)

Answer 1

Answer: 0.105

Explanation:

Binomial probability formula :-

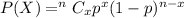`P(X)=^nC_xp^x(1-p)^(n-x)`, here P(X) is the probability of getting success in x trials , n is total trials and p is the probability of getting success in each trial.

Given : The random variable x denotes the number of votes who favor a certain candidate for mayor.

Sample size : n=18

The probability that city's voters favor the candidate: p=0.43

Now, the probability that exactly 10 of the sampled voters favor the candidate is given by :-

`P(X)=^(18)C_(10)(0.43)^(10)(1-0.43)^(8)\\\\=(18!)/(8!10!)(0.43)^(10)(0.57)^8\\\\=0.105375795236approx0.105`

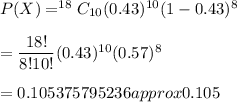
Hence, the probability that exactly 10 of the sampled voters favor the candidate = 0.105