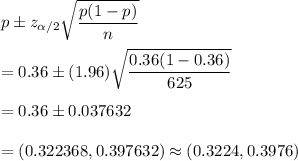Question

In a random sample of 625 people, it was found that 225 of them frequently check their work email when they are at home. Find the upper confidence limit of a 95% confidence interval for p, the true proportion of people who frequently check their work email when they are at home. Give your answer to four decimal places

Answer 1

Answer: (0.3224,0.3976)

Explanation:

Given : Sample size : n=625

Number of people check their work email when they are at home =225

The probability of people check their work email when they are at home :
`p=(225)/(625)=0.36`

Significance level :
`\alpha:1-0.95=0.05`

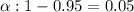
Critical value :
`z_(\alpha/2)=1.96`

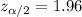
The confidence interval for population proportion is given by :-

`p \pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}\\\\=0.36\pm(1.96)\sqrt{(0.36(1-0.36))/(625)}\\\\=0.36\pm0.037632\\\\=(0.322368,0.397632)\approx(0.3224,0.3976)`