Question

Kevin and Randy Muise have a jar containing 96 ​coins, all of which are either quarters or nickels. The total value of the coins in the jar is ​$14.20 . How many of each type of coin do they​ have?

Answer 1

The number of quarters is 47 and the number of nickels is 49.

Step-by-step explanation:

Let the number of quarters be x and the number of nickels be y.

Kevin and Randy Muise have a jar containing 96 ​coins, all of which are either quarters or nickels.

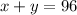`x+y=96` .... (1)

1 quarters = 0.25 dollars

1 nickels = 0.05 dollars

The total value of the coins in the jar is ​$14.20.

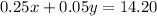`0.25x+0.05y=14.20` .... (2)

From (1) and (2), we get

`0.25(96-y)+0.05y=14.20`

`2400-25y+5y=1420`

`-20y=-980`

`y=49`

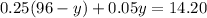
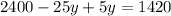
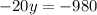
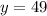
Put this value in equation (1).

`x+49=96`

`x=96-49`

`x=47`

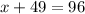
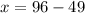
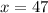
The value of x is 47 and the value of y is 49. Therefore the number of quarters is 47 and the number of nickels is 49.