Question

Gold has a face-centered cubic arrangement with a unit cell edge length of 4.08 Å . How many moles of gold fit in a gold nanoparticle sheet with a length of 68.1 nm , a width of 28.8 nm , and a thickness of 7.78 nm ?

Answer 1

Step-by-step explanation:

As gold sheet will be in the form of a rectangle so, volume of the gold sheet will be as follows.

Volume = length × breadth × height

As given values are length is 68.1 nm, breadth or width is 28.8 nm, and height is 7.78 nm.

Putting these values into the above formula to calculate the volume as follows.

Volume = length × breadth × height

= 68.1 nm × 28.8 nm × 7.78 nm

= 15258.75
`nm^(3)`

As 1 nm =
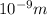`10^(-9) m`. Hence, converting volume into meter as follows.

15258.75
`nm^(3) * \frac{10{-27}m^(3)}{1 nm^(3)}`

=
`1.52 * 10_(-23) m^(3)`

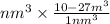
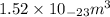
It is given that unit cell edge length is 4.08
`^(o)A` =
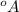`4.08 * 10^(-10) m` m

Volume of a unit cell =
`a^(3)` =
`(4.08 * 10^(-10)m)^(3)`

=
`6.79 * 10^(-29) m^(3)`

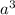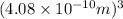
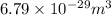
So, number of unit cells in the gold sheet =
`\frac{\text{volume of gold sheet}}{\text{volume of unit cell}}`

=
`(1.52 * 10_(-23))/(6.79 * 10^(-29) m^(3))`

=
`0.223 * 10^(6)`

=
`2.23 * 10^(5)`

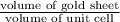
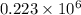
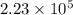
A face-centerd cubic cell contain 4 atoms of gold.

Hence, number of atoms in the sheet are calculated as follows.

`4 * 2.23 * 10^(5)`

=
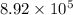`8.92 * 10^(5)` gold atoms

As 1 mol contains
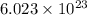`6.023 * 10^(23)` atoms. So, number of moles in
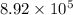`8.92 * 10^(5)` gold atoms will be calculated as follows.

No. of moles of gold atoms in the sheet =
`(8.92 * 10^(5))/(6.023 * 10^(23))`

=
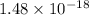`1.48 * 10^(-18)` mol

Thus, we can conclude that given fcc arrangement has
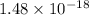`1.48 * 10^(-18)` moles of gold atoms.