Question

A flexible loop has a radius of 10.5 cm and it is in a magnetic field of B = 0.117 T. The loop is grasped at points A and B and stretched until its area is zero. It takes 0.243 s to close the loop. What is the magnetic flux ΦB through the loop before it is streched? Tries 0/20 What is the magnetic flux through the loop after it is stretched? Tries 0/20 What is the magnitude of the average induced electromotive force ε in the loop during the stretching process?

Answer 1

Step-by-step explanation:

Given that,

Radius = 10.5 cm

Magnetic field = 0.117 T

Time = 0.243 s

After stretched, area is zero

(I). We need to calculate the magnetic flux through the loop before stretched

Using formula of magnetic flux

`\phi=B* A`

`\phi=B* \pi r^2`

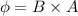
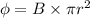
Where, B = magnetic field

r = radius

Put the value into the formula

`\phi=0.117*3.14*(10.5*10^(-2))^2`

`\phi=4.05*10^(-3)\ Tm^2`

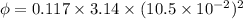
(II). We need to calculate the magnetic flux through the loop after stretched

`\phi=B* A`

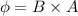
Here, A = 0

`\phi=0`

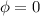
So, The magnetic flux through the loop after stretched is zero.

(III). We need to calculate the magnitude of the average induced electromotive force

Using formula of the induced electromotive force

`\epsilon=-(d\phi)/(dt)`

`\epsilon=-(\phi_(after)-\phi_(before))/(t)`

`\epsilon=-(0-4.05*10^(-3))/(0.243)`

`\epsilon =16.67*10^(-3)\ V`

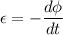
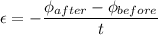
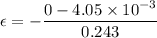
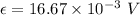
Hence, This is the required solution.