Question

The midpoint of AC is

Answer 1

The midpoint of
`AC` is
`E`.

Hope this helps.

r3t40

Answer 2

Explanation:

Given ABCD is a parallelogram

To prove ⇒ AC trisects BD, and BD bisects AC.

Proof ⇒ Since coordinates of points A, B, C and D have been given in the diagram. If we prove that midpoint of AC and BD are common then AC and BD will equally bisect each other.

Midpoint of AC =
`((x+x')/(2),(y+y')/(2))`

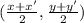
coordinates of A and C are (0,0) and (2a + 2b, 2c)

Now mid point
`E=((2a+2b+0)/(2),(2c+0)/(2))`

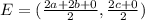
= [(a+b),c]

Now mid point of BD =
`((2b+2a)/(2),(2c+0)/(2))`

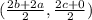
= [(b+a), c]

It proves that midpoints of AC and BD are common.

So AC trisects BD and BD bisects AC.