Question

About 10% of the population has a particular genetic mutation. 700 people are randomly selected. Find the standard deviation for the number of people with the genetic mutation in such groups of 700.

Answer 1

Answer: 7.94

Explanation:

The formula to calculate the standard deviation for binomial distribution :-

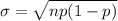`\sigma=√(np(1-p))`, where n is the number total of trials and p is the probability of getting success in each trial.

Given : The probability of the population has a particular genetic mutation=0.1

If 700 people are randomly selected, then the standard deviation for the number of people with the genetic mutation in such groups of 700 will be :-

`\sigma=√(700*0.1(1-0.1))\\\\\Rightarrow\sigma=√(63)\\\\\Rightarrow\sigma=7.9372539331\approx7.94`

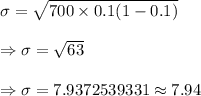
Hence, the standard deviation for the number of people with the genetic mutation in such groups of 700 = 7.94