Question

How many solutions does the system

have?
You can use the interactive graph below to
find the answer.
y = 3x + 3
y= –2x +3

Answer 1

To solve the system of equations we need to use elimination. But to do that we are required to rewrite the equations in implicit form.

`ax+by+c=0`

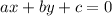
So we have,

`3x-y+3=0 \\ -2x-y+3=0`

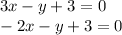
Then multiply the first equation by 2 on both sides and second equation by 3 on both sides. Resulting with,

`6x-2y+6=0 \\ -6x-3y+9=0`

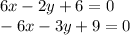
Adding these two equations eliminates the first term in both since 6x - 6x = 0. Hence,

`-5y+15=0\Longrightarrow y=3`

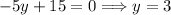
Now that we know the value of y we can insert it in either one of the equations in the system. I'll pick first one to get x.

`3=3x+3\Longrightarrow 3x=0\Longrightarrow x=0`

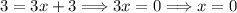
So the solution to this system of equation are
`\boxed{x=0},\boxed{y=3}`

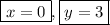
Hope this helps.

r3t40

Answer 2

one solution (0, 3)

Explanation:

The left sides of both equations are equal, so you can equate the right sides

3х + 3 = -2х + 3

3х + 2х = 3 - 3

5х = 0

х = 0

Put value of x in equation 1 to find value of y

y = 3x + 3 = 3*0 + 3 = 3

Тhe system of equations has one solution (0, 3)