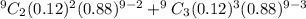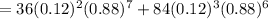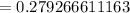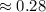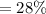Question

Twelve percent of U.S. residents are in their forties. Consider a group of nine U.S. residents selected at random. Find the probability that two or three of the people in the group are in their forties.

Answer 1

The probability is 28 % ( approx )

Explanation:

Since, there are only two possible outcomes in every trails ( residents are in their forties or not ),

So, this is a binomial distribution,

Binomial distribution formula,

Probability of success in x trials,

`P(x)=^nC_x p^x q^(n-x)`

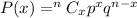
Where,
`^nC_x=(n!)/(x!(n-x)!)`

p and q are probability of success and failure respectively and n is the total number of trials.

Let X be the event of resident who are in his or her forties.

Here, p = 12% = 0.12,

⇒ q = 1 - p = 1 - 0.12 = 0.88,

n = 9,

Hence, the probability that two or three of the people in the group are in their forties = P(X=2) + P(X=3)

`^9C_2 (0.12)^2 (0.88)^(9-2)+^9C_3 (0.12)^3 (0.88)^(9-3)`

`=36(0.12)^2 (0.88)^7+84(0.12)^3 (0.88)^6`

`=0.279266611163`

`\approx 0.28`

`=28\%`