Question

License plates in the great state of Utah consist of 2 letters and 4 digits. Both digits and letters can repeat and the order in which the digits and letters matter. Thus, AA1111 and A1A111 are different plates. How many possible plates are there?

Question options:

non of the above

36^6

26^2x10^4x15

26x26x10x10x10x10

Answer 1

The correct option is 3.

Explanation:

It is given that License plates in the great state of Utah consist of 2 letters and 4 digits.

Total number of letters (A,B,...,Z) = 26

Total number of digits (0,1,2..,9)= 10

Total ways to select a letter is 26 and total ways to select a digit is 10. So, total number of ways to select 2 letter and 4 digits is

`26* 26* 10* 10* 10* 10=26^2* 10^4`

Total ways to arrange these two 2 letter and 4 digits are

`(6!)/(4!2!)=15`

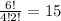
Because total number of places are 6. In which letter can be repeated 2 times and digit can be repeated 4 times.

Total possible plates are

`26^2* 10^4* 15`

Therefore the correct option is 3.