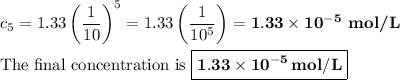Question

A student performed a serial dilution on a stock solution of 1.33 M NaOH. A 2.0 mL aliquot of the stock NaOH (ms) was added to 18 mL of water to make the first dilution (m1). Next, 2.0 mL of the m1 solution was added to 18 mL of water to make the second solution (m2). The same steps were repeated for a total of 5 times. What is the final concentration of NaOH (m5)?

Answer 1

`\boxed{1.33 * 10^(-5)\, \text{mol/L}}}`

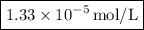
Step-by-step explanation:

Data:

c₀ = 1.33 mol·L⁻¹

Dilutions = 2 mL stock + 18 mL water

n = five dilutions

Calculations:

The general formula is for calculating a single dilution ratio (DR) is

`DR = (V_(i))/(V_(f))`

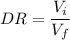
For your dilutions,

`V_(i) = \text{2 mL}\\V_(f) = \text{20 mL}\\DR = \frac{ \text{2 mL}}{\text{20 mL}} = (1)/(10)`

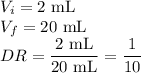
(Note: This is the same as a dilution factor of 10:1)

The general formula for the concentration cₙ after n identical serial dilutions is

`c_(n) = c_(0)(\text{DR})^(n)`

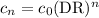
So, after five dilutions

`c_(5) =1.33 \left ((1)/(10) \right )^(5)=1.33\left ( (1)/(10^(5)) \right ) = \mathbf{1.33 * 10^(-5)}\textbf{ mol/L}\\\\\text{The final concentration is $\boxed{\mathbf{1.33 * 10^(-5)\, mol/L}}$}`