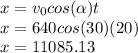Answer:
a)
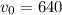 ft/s
ft/s
b)
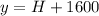 ft where
ft where
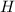 represents the height as the projectile was launched.
represents the height as the projectile was launched.
c)
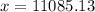 ft
ft
Step-by-step explanation:
First, recognize the values that are given in the problem:
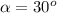
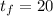
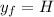
a) With those three use this formula:
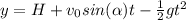
to find the initial velocity
 .
.
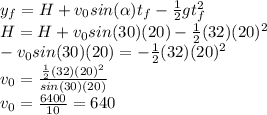
b) In order to find the maximum altitude, the time is needed to apply the formula. The maximum altitude is when the velocity in the y-axis is equal to zero, so use the formula for the velocity in the y-axis is to find the time, the formula is:

With
 s use this formula for the altitude:
s use this formula for the altitude:
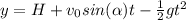
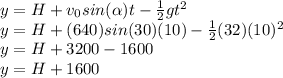
Finally, the range is the maximum displacement in the x-axis, the formula of the displacement is:
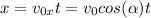
And the maximum occurs when
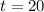 s
s