Question

Multiply 3/sqrt17- sqrt2 by which fraction will produce an equivalent fraction with rational denominator

Answer 1

B.

Explanation:

To simplify something that looks like
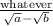`\frac{\text{whatever}}{√(a)-√(b)}` you would multiply the top and bottom by the conjugate of the bottom. So you multiply the top and bottom for this problem I just made by:

`√(a)+√(b)`.

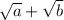If you had
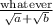`\frac{\text{whatever}}{√(a)+√(b)}`, then you would multiply top and bottom the conjugate of
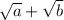`√(a)+√(b)` which is
`√(a)-√(b)`.

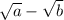The conjugate of a+b is a-b.

These have a term for it because when you multiply them something special happens. The middle terms cancel so you only have to really multiply the first terms and the last terms.

Let's see:

(a+b)(a-b)

I'm going to use foil:

First: a(a)=a^2

Outer: a(-b)=-ab

Inner: b(a)=ab

Last: b(-b)=-b^2

--------------------------Adding.

a^2-b^2

See -ab+ab canceled so all you had to do was the "first" and "last" of foil.

This would get rid of square roots if a and b had them because they are being squared.

Anyways the conjugate of
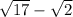`√(17)-√(2)` is

`√(17)+√(2)`.

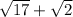This is the thing we are multiplying and top and bottom.

Answer 2

For this case we have the following expression:

`\frac {3} {\sqrt {17} - \sqrt {2}}`

We must rationalize the expression, so we multiply by:

`\frac {\sqrt {17} + \sqrt {2}} {\sqrt {17} + \sqrt {2}}`

So, we have:

`\frac {3} {\sqrt {17} - \sqrt {2}} * \frac {\sqrt {17} + \sqrt {2}} {\sqrt {17} + \sqrt {2}} =\\\frac {3 (\sqrt {17} + \sqrt {2}} {17- \sqrt {17} * \sqrt {2} + \sqrt {17} * \sqrt {2} -2} =\\\frac {3 (\sqrt {17} + \sqrt {2}} {15}`

Thus, the correct option is option B.

Answer:

OPTION B