The formula for distance between two points is:
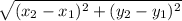
In this case:
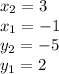
^^^Plug these numbers into the formula for distance like so...
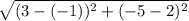
To solve this you must use the rules of PEMDAS (Parentheses, Exponent, Multiplication, Division, Addition, Subtraction)
First we have parentheses. Remember that when solving you must go from left to right
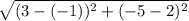
3 - (-1) = 4
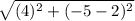
-5 - 2 = -7

Next solve the exponent. Again, you must do this from left to right

4² = 16
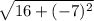
(-7)² = 49
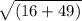
Now for the addition
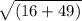
16 + 49 = 65
√65 <<<This can not be further simplified so this is your exact answer
Your approximate answer would be about 8.06
***Remember that the above answers are in terms of units
Hope this helped!
~Just a girl in love with Shawn Mendes