Question

Water use in the summer is normally distributed with a mean of 311.4 million gallons per day and a standard deviation of 40 million gallons per day. City reservoirs have a combined storage capacity of 350 million gallons. The probability that a day requires more water than is stored in city reservoirs is P(X > 350)= 1 - P (Z < b). What is the value of b? Please report your answer in 3 decimal places.

Answer 1

Answer: 0.965

Explanation:

Given : Water use in the summer is normally distributed with

`\mu=311.4\text{ million gallons per day}`

`\sigma=40 \text{ million gallons per day}`

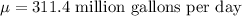
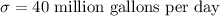
Let X be the random variable that represents the quantity of water required on a particular day.

Z-score :
`(x-\mu)/(\sigma)`

`(350-311.4)/(40)=0.965`

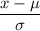
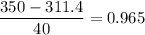
Now, the probability that a day requires more water than is stored in city reservoirs is given by:-

`P(x>350)=P(z>0.965)=1-P(z<0.965)`

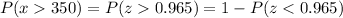
We can see that on comparing the above value to the given P(X > 350)= 1 - P(Z < b) , we get the value of b is 0.965.