Question

Prove that the segments joining the midpoint of consecutive sides of an isosceles trapezoid form a rhombus.

Find the slope of DE and FG.

Answer 1

B. See explanation

Explanation:

Use the distance formula between two points
`(x_1,y_1)` and
`(x_2,y_2):`

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

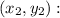
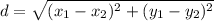
Find the lengths of all sides of quadrilateral DEFG:

`DE=√((-a-b-0)^2+(c-2c)^2)=√((a+b)^2+c^2)\\ \\</p><p>EF=√((a+-b-0)^2+(c-2c)^2)=√((a+b)^2+c^2)\\ \\</p><p>FG=√((a+b-0)^2+(c-0)^2)=√((a+b)^2+c^2)\\ \\</p><p>GD=√((-a-b-0)^2+(c-0)^2)=√((a+b)^2+c^2)\\ \\`

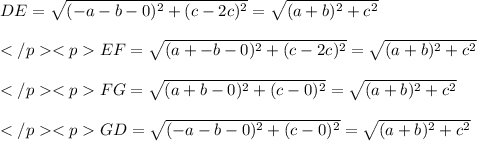
All sides are of the same length. Now fond the slopes of all sides:

`DE=(2c-c)/(0-(-a-b))=(c)/(a+b)\\ \\EF=(c-2c)/(a+b-0)=-(c)/(a+b)\\ \\FG=(c-0)/(a+b-0)=(c)/(a+b)\\ \\GD=(c-c)/(-a-b-0)=-(c)/(a+b)\\ \\`

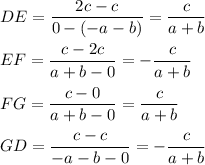
The slopes of the sides DE and FG are the same, so these sides are parallel. The slopes of the sides EF and GD are the same, so these sides are parallel.