Question

When purchasing bulk orders of​ batteries, a toy manufacturer uses this acceptance sampling​ plan: Randomly select and test 56 batteries and determine whether each is within specifications. The entire shipment is accepted if at most 2 batteries do not meet specifications. A shipment contains 7000 ​batteries, and 1​% of them do not meet specifications. What is the probability that this whole shipment will be​ accepted? Will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

98.1% chance of being accepted

Explanation:

Given:

sample size,n=56

acceptance condition= at most 2 batteries do not meet specifications

shipment size=7000

battery percentage in shipment that do not meet specification= 1%

Applying binomial distribution

P(x)=∑ᵇₐ=₀ (n!/a!(n-a)!)p^a (1-p)^(n-a)

In this formula, a is the acceptable number of defectives;

n is the sample size;

p is the fraction of defectives in the population.

Now putting the value

a= 2

n=56

p=0.01

`(56!)/(0!\left(56-0\right)!)\left(0.01\right)^0\:\left(1-0.01\right)^(\left(56-0\right)) + (56!)/(1!\left(56-1\right)!)\left(0.01\right)^1\:\left(1-0.01\right)^(\left(56-1\right)) +`
`\:(56!)/(2!\left(56-2\right)!)\left(0.01\right)^2\:\left(1-0.01\right)^(\left(56-2\right))`

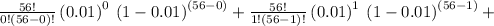
=0.56960+0.32219+0.08949

After summation, we get 0.981 i.e. a 98.1% chance of being accepted. As this is such a high chance, we can expect many of the shipments like this to be accepted!