Question

determine if the point (1,6) is on the circle whose center is (1,1) and includes the point (-3,4)!!!! i need help asap im breaking my head trying to understand this!!!!

Answer 1

Point (1 , 6) is on the circle

Explanation:

* Lets explain how to solve the problem

- The equation of the circle with center (h , k) and radius r is:

(x - h)² + (y - k)² = r²

- To prove that a point lies on the circle , substitute x , y in the

equation by the coordinates of this point if the left hand side of

the equation equals the right hand side that means the point

satisfies the equation then the point lies on the circle

* Lets use this fact to solve the problem

∵ The center of the circle is (1 , 1)

∴ h = 1 , k = 1

∵ The point (-3 , 4) lies on the circle

∴ The distance between the center of the circle (1 , 1) and the point

(-3 , 4) is the radius of the circle

- The rule of the distance between points(x1 , y1) and (x2 , y2) is

d = √[(x2 - x1)² + (y2 - y1)²]

∵ (1 , 1) is (x1 , y1) and (-3 , 4) is (x2 , y2)

∴ x1 = 1 , x2 = -3 and y1 = 1 , y2 = 4

- Lets calculate r using the rule of the distance above

∴
`r=\sqrt{(-3 -1)^(2)+(4-1)^(2)}=\sqrt{(-4)^(2)+(3)^(2)}=√(16+9)=√(25)=5`

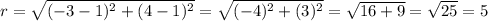
∴ The radius of the circle is 5 units

∵ The equation of the circle is (x - h)² + (y - k)² = r²

∵ h = 1 , k = 1 , r = 5

∴ (x - 1)² + (y - 1)² = 25

∴ The equation of the circle is (x - 1)² + (y - 1)² = 25

- Lets substitute x and y in the equation by the coordinates of

point (1 , 6)

∵ x = 1 and y = 6

∵ L.H.S ⇒ (1 - 1)² + (6 - 1)² = (0)² + (5)² = 0 + 25 = 25

∵ R.H.S ⇒ 25

∴ L.H.S = R.H.S

∴ Point (1 , 6) is on the circle