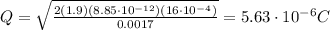Answer:
Step-by-step explanation:
The capacitor of a parallel-plate capacitor is given by:
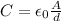
where
A is the area of each plate
d is the separation between the plates
 is the vacuum permittivity
is the vacuum permittivity
The energy stored in a capacitor instead is given by
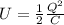
where
Q is the charge stored in each plate
Substituting the expression we found for C inside the last formula,
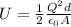
And re-arranging it

Now if we substitute
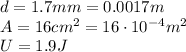
We find the charge stored on the capacitor: