Answer : The percent composition by volume of mixture of
 and
and
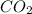 are, 18.94 % and 81.06 % respectively.
are, 18.94 % and 81.06 % respectively.
Solution :
According to the Graham's law, the rate of effusion of gas is inversely proportional to the square root of the molar mass of gas.

And the relation between the rate of effusion and volume is :
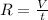
or, from the above we conclude that,
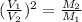 ..........(1)
..........(1)
where,
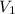 = volume of helium gas = 29.7 ml
= volume of helium gas = 29.7 ml
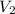 = volume of mixture = 9.28 ml
= volume of mixture = 9.28 ml
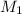 = molar mass of helium gas = 4 g/mole
= molar mass of helium gas = 4 g/mole
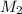 = molar mass of mixture = ?
= molar mass of mixture = ?
Now put all the given values in the above formula 1, we get the molar mass of mixture.


The average molar mass of mixture = 40.97 g/mole
Now we have to calculate the percent composition by volume of the mixture.
Let the mole fraction of
 be, 'x' and the mole fraction of
be, 'x' and the mole fraction of
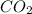 will be, (1 - x).
will be, (1 - x).
As we know that,


Now put all the given values in this expression, we get:

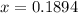
The mole fraction of
 = x = 0.1894
= x = 0.1894
The mole fraction of
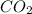 = 1 - x = 1 - 0.1894 = 0.8106
= 1 - x = 1 - 0.1894 = 0.8106
The percent composition by volume of mixture of
 =
=

The percent composition by volume of mixture of
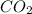 =
=
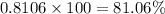
Therefore, the percent composition by volume of mixture of
 and
and
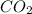 are, 18.94 % and 81.06 % respectively.
are, 18.94 % and 81.06 % respectively.