Question

Find X

Options:

6
4 square root 6
6
square root 146

Answer 1

x=4√6

Explanation:

We can see that the given triangle is converted into two right angled triangles with x.

We can use any one triangle to find x.

IT can also be seen that the base's length is equally divided on both sides of x.

So

b = 10/2 = 5

h = 11

p = x

Using the Pythagoras theorem

`h^2 = b^2+p^2\\(11)^2 = (5)^2+p^2\\121=25+p^2\\121-25 = p^2\\96=p^2\\Taking\ square\ root\ on\ both\ sides\\√(96)=√(p^2)\\p=√(96) \\p=√(16*6)\\ p=4\sqrt6`

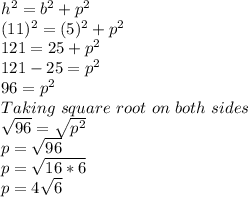
Therefore

x=4√6 ..

Answer 2

For this case we can apply the Pythagorean theorem to find "x". Taking the rectangle triangle of base 5 we have:

`x = \sqrt {11 ^ 2-5 ^ 2}\\x = \sqrt {121-25}\\x = \sqrt {96}\\\x = \sqrt {4 ^ 2 * 6}`

By definition of power properties we have:

`\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}`

So:

`x = 4 \sqrt {6}`

Answer:

`x = 4 \sqrt {6}`