Answer:
Assume that
 and
and
 are constants. The slope of the line will be equal to
are constants. The slope of the line will be equal to
Explanation:
Rewrite the expression of the line to express
 in terms of
in terms of
 and the constants.
and the constants.
Substract
 from both sides of the equation:
from both sides of the equation:
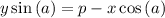 .
.
In case
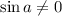 , divide both sides with
, divide both sides with
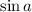 :
:
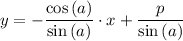 .
.
Take the first derivative of both sides with respect to
 .
.
 is a constant, so its first derivative will be zero.
is a constant, so its first derivative will be zero.
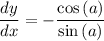 .
.
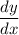 is the slope of this line. The slope of this line is therefore
is the slope of this line. The slope of this line is therefore
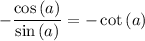 .
.
In case
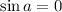 , the equation of this line becomes:
, the equation of this line becomes:
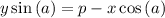 .
.
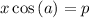 .
.
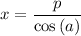 ,
,
which is the equation of a vertical line that goes through the point
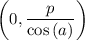 . The slope of this line will be infinity.
. The slope of this line will be infinity.