Question

Plzzz hurry up and help me if A+B=45
prove that
(1+tanA)(1+tanB)=2​

Answer 1

see explanation

Explanation:

If A +B = 45° then tan(A+B) = tan45° = 1

Expanding (1 + tanA)(1 + tanB)

= 1 + tanA + tanB + tanAtanB → (1)

Using the Addition formula for tan(A + B)

tan(A+B) =
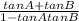`(tanA+tanB)/(1-tanAtanB)` = 1 ← from above

Hence

tanA + tanB = 1 - tanAtanB ( add tanAtanB to both sides )

tanA + tanB + tanAtanB = 1 ( add 1 to both sides )

1 + tanA + tanB + tanAtanB = 2

Then from (1)

(1 + tanA)(1 + tanB) = 2 ⇒ proven