Question

Radar uses radio waves of a wavelength of 2.9 m . The time interval for one radiation pulse is 100 times larger than the time of one oscillation; the time between pulses is 10 times larger than the time of one pulse. What is the shortest distance to an object that this radar can detect? Express your answer with the appropriate units.

Answer 1

145 m

Step-by-step explanation:

Given:

Wavelength (λ) = 2.9 m

we know,

c = f × λ

where,

c = speed of light ; 3.0 x 10⁸ m/s

f = frequency

thus,

`f=(c)/(\lambda)`

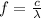
substituting the values in the equation we get,

`f=(3.0* 10^8 m/s)/(2.9m)`

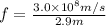
f = 1.03 x 10⁸Hz

Now,

The time period (T) =
`(1)/(f)`

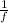
or

T =
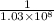`(1)/(1.03* 10^8)` = 9.6 x 10⁻⁹ seconds

thus,

the time interval of one pulse = 100T = 9.6 x 10⁻⁷ s

Time between pulses = (100T×10) = 9.6 x 10⁻⁶ s

Now,

For radar to detect the object the pulse must hit the object and come back to the detector.

Hence, the shortest distance will be half the distance travelled by the pulse back and forth.

Distance = speed × time = 3 x 10^8 m/s × 9.6 x 10⁻⁷ s) = 290 m {Back and forth}

Thus, the minimum distance to target =
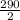`(290)/(2)` = 145 m