Question

Enter your PIN: The technology company DataGenetics suggests that % of all four-digit personal identification numbers, or PIN codes, have a repeating digits format such as . Assuming this to be true, if the PIN codes of seven people are selected at random, what is the probability that at least one of them will have repeating digits? Round your answer to four decimal places.

Answer 1

Answer: 0.9917

Explanation:

If repetition is allowed , then the total number of possible four digits pin codes =
`10^4=10,000`

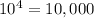
Number of ways to make for digit code without repetition of digits =

`10*9*8*7=5040`

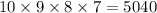
Number of ways to make for digit codes having repetition =

`10,000-5040=4960`

Probability that a person has pin code that has repetition:-

`(4960)/(10,000)=0.496`

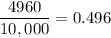
Let x be number of pin codes with repeating digits.

If the PIN codes of seven people are selected at random, then the probability that at least one of them will have repeating digits:-

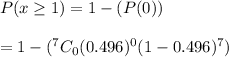`P(x\geq1)=1-(P(0))\\\\=1-(^7C_0(0.496)^0(1-0.496)^7)` (By Binomial distribution)

`=1-((0.496)^0(0.504)^7)=0.991739358875\approx0.9917`

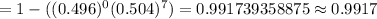
Hence, the probability that at least one of them will have repeating digits = 0.9917