Question

Suppose that administrators of a large school district wish to estimate the proportion of children in the district enrolling in kindergarten who attended preschool. They took a simple random sample of children in the district who are enrolling in kindergarten. Out of 75 children sampled, 51 had attended preschool. Construct a large-sample 99% z ‑confidence interval for p, the proportion of all children enrolled in kindergarten who attended preschool. Give the limits of the confidence interval as decimals, precise to at least three decimal places.

Answer 1

Answer: (0.541, 0.819)

Explanation:

The confidence interval for proportion is given by :-

`p\pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}`

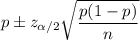
Given : The proportion of children attended the school =
`p=(51)/(75)=0.68`

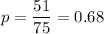
Significance level :
`\alpha=1-0.99=0.01`

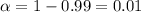
Critical value :
`z_(\alpha/2)=z_(0.005)=\pm2.576`

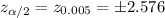
Now, the 99% z ‑confidence interval for proportion will be :-

`0.68\pm (2.576)\sqrt{(0.68(1-0.68))/(75)}\approx0.68\pm 0.139\\\\=(0.68-0.139,0.68+0.139)=(0.541,\ 0.819)`

Hence, the 99% z ‑confidence interval for p, the proportion of all children enrolled in kindergarten who attended preschool = (0.541, 0.819)