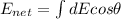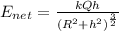Question

A thin ring of radius R is uniformly charged with the total positive charge Q. 1. Find the electric field at distance h right above the center of the ring

Answer 1

`E_(net) = \frac{k Q h}{(R^2 + h^2)^{(3)/(2)}}`

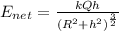
Step-by-step explanation:

If charge Q is uniformly distributed over the ring then for small element of the ring the charge will be given as

`dq = (Q)/(2\pi R) dL`

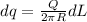
now electric field due to this small element on the axis of ring at height "h" is given as

`dE = (k dq)/(R^2 + h^2)`

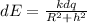
now since this electric field is radially in the direction of joining the position of charge to the given point

so net field due to ring will be along the axis of ring

so we have

`E_(net) = \int dEcos\theta`

`E_(net) = \int (k dq)/(R^2 + h^2) (h)/(√(R^2 + h^2))`

`E_(net) = \frac{k Q h}{(R^2 + h^2)^{(3)/(2)}}`