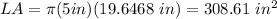The traffic cone is 19 inches tall & has a radius of 5 inches. Find the lateral area.

Question

asked Jun 2, 2020 211k views

2 Answers

Suman · Answer 1 · 2020-06-04T10:21:01+0000

Answer:
$308.61\ in^2$

Explanation:

In order to calculate the lateral area of the traffic cone, we can use the following formula:

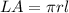
$LA=\pi rl$

Where "r" is the radius and "l" is the slant height of the cone.

We need to find the slant height. Knowing the height and the radius, we can calculate it with the Pythagorean Theorem:

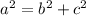
a^2=b^2+c^2

Where "a" is the hypotenuse and "b" and "c" are the legs of the triangle.

For this case, we can say that:

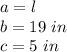
$a=l\\b=19\ in\\c=5\ in$

Substituting anf solviing for "l", we get:

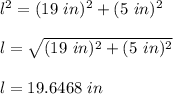
$l^2=(19\ in)^2+(5\ in)^2\\\\l=√((19\ in)^2+(5\ in)^2)\\\\l=19.6468\ in$

Now we can substitute values into the formula for calculate the lateral area of the traffic cone. This is:

$LA=\pi (5 in)(19.6468\ in)=308.61\ in^2$