Answer: 0.0192
Explanation:
Given : The mean per capita consumption of milk per year :
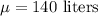
Standard deviation :
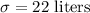
Sample size :
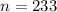
Let
 be the sample mean.
be the sample mean.
The formula for z-score in a normal distribution :
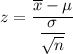
For


The P-value =
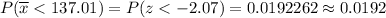
Hence, the probability that the sample mean would be less than 137.01 liters is 0.0192 .