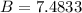Question

Two vectors A⃗ and B⃗ are at right angles to each other. The magnitude of A⃗ is 5.00. What should be the length of B⃗ so that the magnitude of their vector sum is 9.00?

Answer 1

Length of B is 7.4833

Explanation:

The vector sum of A and B vectors in 2D is

`C=A+B=(a_1+b_1,a_2+b_2)`

And its magnitude is:

`C=√((a_1+b_1)^2+(a_2+b_2)^2) =9`

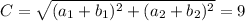
Where

`a_1=Asinx`

`a_2=Acosx`

`b_1=Bsin(x+90)`

`b_2=Bcos(x+90)`

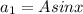
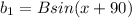
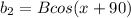
Using the properties of the sum of two angles in the sin and cosine:

`b_1=Bsin(x+90)=B(sinx*cos90+sin90*cosx)=Bcosx`

`b_2=Bcos(x+90)=B(cosx*cos90-sinx*sin90)=-Bsinx`

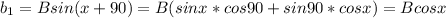
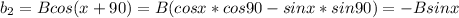
Sustituying in the magnitud of the sum

`C=√((Asinx+Bcosx)^2+(Acosx-Bsinx)^2) =9`

`C=√(A^2sin^2x+2ABsinxcosx+B^2cos^2x+A^2cos^2x-2ABsinxcosx+B^2sin^2x) =9`

`C=√(A^2(sin^2x+cos^2x)+B^2(cos^2x+sin^2x))`

`C=√(A^2+B^2) =9`

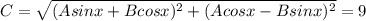
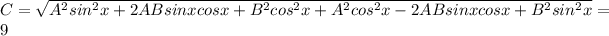
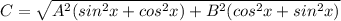
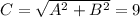
Solving for B

`A^2+B^2 =9^2`

`B^2 =9^2-A^2`

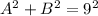
Sustituying the value of the magnitud of A

`B^2=81-5^2=81-25=56`

`B= 7. 4833`