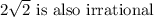Question

To which subsets of the real numbers does 2 radical 2 belong?

(a) Natural
b) Whole
c) Irrational
d) Integers
e) Rational

Answer 1

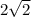`2√(2)` is irrational .

Explanation:

The Natural numbers are {1,2,3,4,5,6,7,....}.

Natural numbers are also called counting numbers because they are numbers people use to count with.

Whole numbers are almost the same as natural numbers. They include one extra number which is 0.

So the whole numbers are {0,1,2,3,4,5,6,7,...}.

Irrational numbers are real numbers that aren't rational numbers.

Rational numbers are number that can be written as fractions where the numerator and denominator are integers (bottom integer is not 0).

Terminating decimals, repeating decimals, and integers all can be written this way which makes them rational.

Integers are numbers in the set {...,-4,-3,-2,-1,0,1,2,3,4,...}. So these are your counting numbers, 0, and the opposite of your counting numbers.

You want to figure out which set does
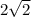`2√(2)` belong to.

You cannot simplify this number anymore than it is. So this is definitely not a number you can count to. It is not the opposite of a counting number. It is also not 0. We have ruled out the following sets: Natural, whole, and integers.

So it is between rational and irrational.

`√(a) \text{ is irrational if } a \text{ is not a perfect square}`.

`√(a) \text{ is rational if } a \text{ is a perfect square}`.

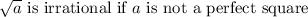2 is not a perfect square.

`√(2) \text{ is irrational}`

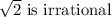
So
`2√(2) \text{ is also irrational}`