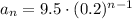Question

What is the explicit rule for the geometric sequence?

9.5,1.9,0.38,0.076,...

Answer 1

`a_n=9.5 \cdot (0.2)^(n-1)`

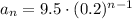
Explanation:

If this is a geometric sequence, it will have a common ratio.

The common ratio can be found by dividing term by previous term.

The explicit form for a geometric sequence is
`a_n=a_1 \cdot r^(n-1) \text{ where } a_1 \text{ is the first term and } r \text{ is the common ratio}`

We are have the first term is
`a_1=9.5`.

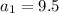Now let's see this is indeed a geometric sequence.

Is 0.076/0.38=0.38/1.9=1.9/9.5?

Typing each fraction into calculator and see if you get the same number.

Each fraction equal 0.2 so the common ratio is 0.2.

So the explicit form for our sequence is

`a_n=9.5 \cdot (0.2)^(n-1)`