Answer:
The value of
 is
is
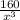 .
.
Explanation:
The given equation is
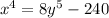
We need to find the value of
 .
.
Differentiate with respect to t.
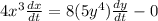
![[\because (d)/(dx)x^n=nx^(n-1),(d)/(dx)C=0]](https://img.qammunity.org/2020/formulas/mathematics/college/wr7v8gz835e8twpqdm4w0gw2ofw0cq0wcb.png)
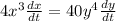
It is given that y=2 and dy/dt=1, substitute these values in the above equation.
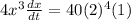

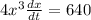
Divide both sides by 4x³.
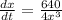
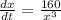
Therefore the value of
 is
is
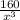 .
.