Question

An undiscovered planet, many light-years from Earth, has one moon which has a nearly circular periodic orbit. If the distance from the center of the moon to the surface of the planet is 2.31500 x 10^5 km and the planet has a radius of 4.150 x10^3 km and a mass of 7.15 x10^22 kg, how long (in days) does it take the moon to make one revolution around the planet. The gravitational constant is 6.67 x10^-11 N m^2/kg^2.

Answer 1

118.06 days

Step-by-step explanation:

d = distance of the center of moon from surface of planet = 2.315 x 10⁵ km = 2.315 x 10⁸ m

R = radius of the planet = 4.15 x 10³ km = 4.15 x 10⁵ m

r = center to center distance between the planet and moon = R + d

M = mass of the planet = 7.15 x 10²² kg

T = Time period of revolution around the planet

Using Kepler's third law

`T^(2)=(4\pi ^(2)r^(3))/(GM)`

`T^(2)=(4\pi ^(2)(R + d)^(3))/(GM)`

`T^(2)=(4(3.14)^(2)((4.15* 10^(5)) + (2.315* 10^(8)))^(3))/((6.67* 10^(-11))(7.15* 10^(22)))`

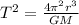
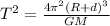
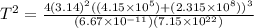
T = 1.02 x 10⁷ sec

we know that , 1 day = 24 h = 24 x 3600 sec = 86400 sec

T =
`(1.02 * 10^(7) sec)(1 day)/(86400 sec)`

T = 118.06 days