Answer:
Proofs are in the explantion.
Explanation:
We are given the following:
1)
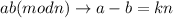 for integer
for integer
 .
.
1)
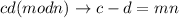 for integer
for integer
 .
.
a)
Proof:
We want to show
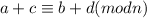 .
.
So we have the two equations:
a-b=kn and c-d=mn and we want to show for some integer r that we have
(a+c)-(b+d)=rn. If we do that we would have shown that
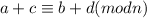 .
.
kn+mn = (a-b)+(c-d)
(k+m)n = a-b+ c-d
(k+m)n = (a+c)+(-b-d)
(k+m)n = (a+c)-(b+d)
k+m is is just an integer
So we found integer r such that (a+c)-(b+d)=rn.
Therefore,
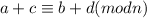 .
.
//
b) Proof:
We want to show
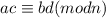 .
.
So we have the two equations:
a-b=kn and c-d=mn and we want to show for some integer r that we have
(ac)-(bd)=tn. If we do that we would have shown that
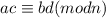 .
.
If a-b=kn, then a=b+kn.
If c-d=mn, then c=d+mn.
ac-bd = (b+kn)(d+mn)-bd
= bd+bmn+dkn+kmn^2-bd
= bmn+dkn+kmn^2
= n(bm+dk+kmn)
So the integer t such that (ac)-(bd)=tn is bm+dk+kmn.
Therefore,
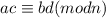 .
.
//