Question

The height of a cone is twice the radius of its base. What expression represents the volume of the cone, in cubic units?

Answer 1

`V=(1)/(3)\pi r^2h\\\\h=2r\\V=(1)/(3)\pi r^2\cdot(2r)=(2)/(3)\pi r^3`

Answer 2

`V=(2)/(3)\pi R^(3)`

Explanation:

The Volume of a cone is by definition 1/3 of the volume of a Cylinder. In this question, the height equals to diameter (2R).

So, We have:

`h_(cone)=2R\\V=(1)/(3)\pi R^(2)h \Rightarrow V=(1)/(3)\pi R^(2)2R \Rightarrow V=(2)/(3)\pi R^(3)`

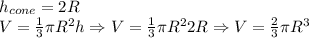
We conclude that under this circumstance, a cone with a height equal to its diameter will turn its volume to be equal to 2/3 of pi times the radius raised to the third power.

In other words, when the height is equal to the diameter. The relation between radius, height and Volume changes completely.