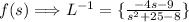
First dismantle,
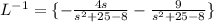
Now use the linearity property of Inverse Laplace Transform which states,
For functions
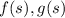 and constants
and constants
 rule applies,
rule applies,
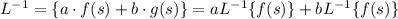
Hence,
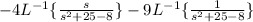
The first part simplifies to,

The second part simplifies to,
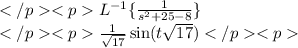
And we result with,
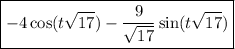
Hope this helps.
If you have any additional questions please ask. I made process of solving as quick as possible therefore you might be left over with some uncertainty.
Hope this helps.
r3t40