Question

If x^2-y^2 = 56 and x-y= 4 then what is the average of x and y

a) 3 b) 7 c) 2 d) 6 e) 4

Answer 1

7

Explanation:

`x^2-y^2` is a difference of squares.

When factoring a difference of squares, you can use this formula
`u^2-v^2=(u-v)(u+v)`.

So
`x^2-y^2` can be factored as
`(x-y)(x+y)`.

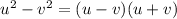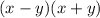So back to the problem:

`x^2-y^2=56`

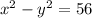
Rewriting with a factored left hand side:

`(x-y)(x+y)=56`

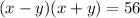
We are given x-y=4 so rewriting again with this substitution:

`4(x+y)=56`

Dividing both sides by 4:

`(x+y)=14`

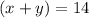
So we have x+y equals 14.

We are asked to find the average of x and y which is (x+y)/2.

So since x+y=14 , then (x+y)/2=14/2=7.