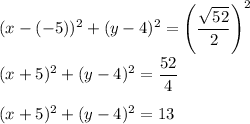Question

Help !! Please I can’t find the answer

Answer 1

`\large\boxed{r^2=(x+5)^2+(y-4)^2}`

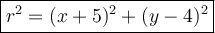
Explanation:

The equation of a circle:

`(x-h)^2+(y-k)^2=r^2`

(h, k) - center

r - radius

We have diameter endpoints.

Half the length of the diameter is the length of the radius.

The center of the diameter is the center of the circle.

The formula of a distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Substitute the coordinates of the given points (-8, 2) and (-2, 6):

`d=√((6-2)^2+(-2-(-8))^2)=√(4^2+6^2)=√(16+36)=√(52)`

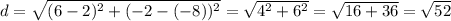
The radius:

`r=(d)/(2)\to r=(√(52))/(2)`

The formula of a midpoint:

`\left((x_1+x_2)/(2),\ (y_1+y_2)/(2)\right)`

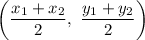
Substitute:

`x=(-8+(-2))/(2)=(-10)/(2)=-5\\\\y=(2+6)/(2)=(8)/(2)=4`

`(-5,\ 4)\to h=-5,\ k=4`

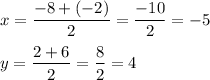
Finally:

`(x-(-5))^2+(y-4)^2=\left((√(52))/(2)\right)^2\\\\(x+5)^2+(y-4)^2=(52)/(4)\\\\(x+5)^2+(y-4)^2=13`