Question

A square has side length of 9 in. If the area is doubled, what happens to the side length?

Answer 1

sq root of 2

Explanation:

that's how Mr. Burger says it is, lol.

because the area is doubled then both side lengths are multiplied by the sq root of 2.

Answer 2

The side length is multiplied by
`√(2)`

Explanation:

we know that

The area of the original square is equal to

`A=9^(2)=81\ in^(2)`

If the area is doubled

then

The area of the larger square is

`A1=(2)81=162\ in^(2)`

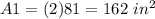
Remember that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z ----> the scale factor

x ----> the area of the larger square

y ---> the area of the original square

so

`z^(2)=(x)/(y)`

we have

`x=162\ in\^(2)`

`y=81\ in\^(2)`

`z^(2)=(162)/(81)`

`z^(2)=2`

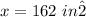
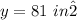
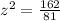
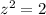
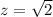`z=√(2)` ------> scale factor

therefore

The side length is multiplied by
`√(2)`