Question

The table shows values for a quadratic function. What is the average rate of change for this function for the interval from x=2 to x=4

Answer 1

Answer: OPTION C.

Explanation:

In order to find the average rate of change for this function for the given quadratic function, for the interval from
`x=2` to
`x=4`, you can use this formula:

`average\ rate\ of\ change`
`=(f(b)-f(a))/(b-a)`

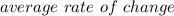
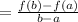
In this case, you can identify that:

`f(b)=8\\f(a)=32\\\\b=2\\\\a=4`

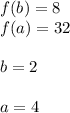
Then, substituting values into the formula, you get this result:

`average\ rate\ of\ change=(8-32)/(2-4)=12`

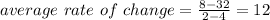
This matches with the option C.

Answer 2

C. 12

EXPLANATION

The average rate of change of a function ,f(x) from x=a to x=b is given by:

`(f(b) - f(a))/(b - a)`

We want to find the average rate of change of the quadratic function represented by the table for the interval from x=2 to x=4.

From the table, we have

`f(4) = 32`

and

`f(2) = 8`

The average rate of is

`(f(4) - f(2))/(4 - 2) = (32 - 8)/(2) = (24)/(2) = 12`

Geometrically, the average rate of change represents the slope of the secant line joining the points (4,32) and (2,8) on the given quadratic function.

The correct choice is C.